फ्रैक्टल्सपरिचय
जब प्रकृति के चारों ओर देखते हैं, तो आपने इन जैसे जटिल पौधों पर ध्यान दिया होगा:


यह {११} फर्न {११ ९} में कई छोटे पत्ते होते हैं जो एक बड़ी शाखा से निकलते हैं।


यह {१२१} रोमनस्को ब्रोकोली {१२२} में छोटे {१२३} शंकु {१२४} होते हैं, जो बड़े आकार के होते हैं।
प्रारंभ में, ये अत्यधिक जटिल आकृतियों की तरह दिखाई देते हैं - लेकिन जब आप करीब देखते हैं, तो आप देख सकते हैं कि वे दोनों एक अपेक्षाकृत सरल पैटर्न का पालन करते हैं: सभी {१२५} व्यक्तिगत हिस्से {१२६} पौधों के बिल्कुल समान दिखते हैं पौधा, बस छोटा। एक ही पैटर्न को छोटे पैमाने पर बार-बार दोहराया जाता है।
गणित में, हम इस संपत्ति को आत्म-समानता कहते हैं, और इसके आकार को
अपने स्वयं के भग्न बनाने के लिए, हमें एक साधारण पैटर्न के साथ शुरू करना होगा और फिर इसे छोटे पैमाने पर बार-बार दोहराना होगा।
सबसे सरल पैटर्नों में से एक लाइन सेगमेंट हो सकता है, दो और सेगमेंट एक सिरे से बंटकर। यदि हम इस पैटर्न को दोहराते हैं, तो इन दोनों नीले खंडों की दो और शाखाएँ होंगी।
आप सभी शाखाओं की लंबाई और कोण को बदलने के लिए नीले डॉट्स को स्थानांतरित कर सकते हैं। फिर
शाखाओं की स्थिति के आधार पर, आप पूरी तरह से अलग पैटर्न बना सकते हैं - ऊपर जैसा लग रहा है, एक , या । और क्या मिल सकता है?
एक और प्रसिद्ध भग्न
ध्यान दें कि अंतिम आकृति से बनी है, जो स्वयं की तीन समान प्रतियाँ हैं, और इनमें से प्रत्येक पूरी त्रिभुज की छोटी प्रतियों से बनी है! आप त्रिकोण में हमेशा के लिए ज़ूम कर सकते हैं, और पैटर्न और आकार हमेशा दोहराते रहेंगे।
इस अध्याय के आरंभ में पौधे भग्न की तरह लगते हैं, लेकिन वास्तविक जीवन में सच भग्न बनाना स्पष्ट रूप से असंभव है। यदि हम एक ही पैटर्न को बार-बार, छोटे और छोटे से दोहराते रहें, तो हम अंततः कोशिकाओं, अणुओं या परमाणुओं को प्राप्त कर लेंगे जिन्हें अब विभाजित नहीं किया जा सकता है।
हालांकि, गणित का उपयोग करते हुए, हम उन गुणों के बारे में सोच सकते हैं जो वास्तविक भग्न "होंगे" - और ये बहुत ही आश्चर्यजनक हैं ... [{:::}
भग्न आयाम
पहले, आइए भग्न के आयाम के बारे में सोचते हैं। एक रेखा का आयाम
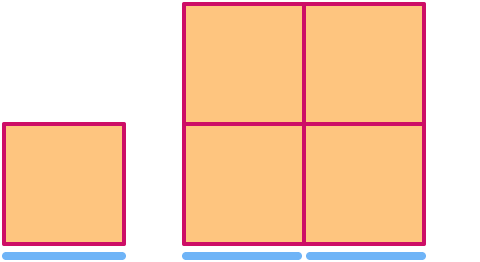
एक वर्ग का आयाम
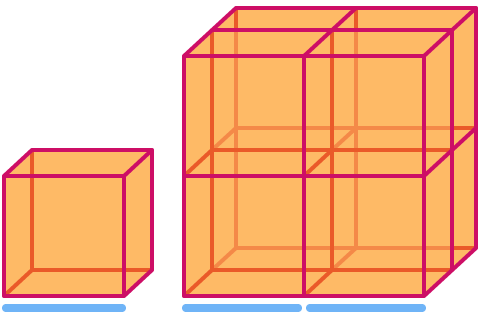
एक घन का आयाम
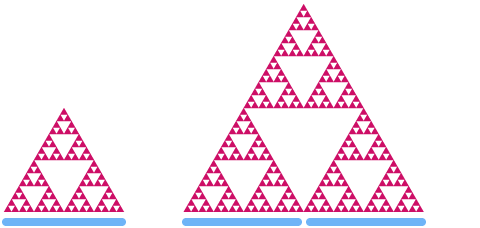
अब चलो Sierpinski त्रिकोण पर एक नजर डालते हैं। यदि हम इसे 2 के कारक से मापते हैं, तो आप देख सकते हैं कि यह "201} 3]] के कारक से" क्षेत्र "बढ़ जाता है।
बता दें कि d Sierpinski त्रिकोण का आयाम है। ऊपर के समान पैटर्न का उपयोग करके, हमें
लेकिन रुकिए ... किसी चीज़ का एक आयाम कैसे हो सकता है जो पूर्णांक नहीं है? यह असंभव लगता है, लेकिन यह भग्न के अजीब गुणों में से एक है। वास्तव में, यह वही है जो भग्न को अपना नाम देता है: उनके पास एक आंशिक आयाम है।
प्रत्येक पुनरावृत्ति के साथ, हम Sierpinski त्रिकोण के कुछ क्षेत्र को हटा देते हैं। यदि हम इसे कई बार कर सकते हैं, तो वास्तव में कोई क्षेत्र नहीं छोड़ा जाएगा: यही कारण है कि सियरपिंस्की त्रिकोण 2-आयामी क्षेत्र और 1-आयामी लाइन के बीच में कुछ है।
जबकि कई फ्रैक्टल्स स्व-समान हैं, एक बेहतर परिभाषा यह है कि फ्रैक्टल्स आकार हैं, जिनमें गैर-पूर्णांक आयाम हैं।
कोच हिमफल
प्रकृति में कई आकृतियाँ हैं जो भग्न की तरह दिखती हैं। हमने पहले ही इस अध्याय की शुरुआत में कुछ पौधों को देखा है। अन्य महान उदाहरण बर्फ के टुकड़े और बर्फ के क्रिस्टल हैं:
अपनी खुद की फ्रैक्टल स्नोफ्लेक बनाने के लिए, हमें एक बार फिर एक सरल प्रक्रिया ढूंढनी होगी जिसे हम बार-बार लागू कर सकते हैं।
Sierpinski त्रिकोण की तरह, एक एकल, एकतरफा त्रिकोण के साथ शुरू करते हैं। हालांकि, हर चरण पर छोटे त्रिकोणों को हटाने के बजाय, हम किनारे के साथ छोटे त्रिकोणों को जोड़ते हैं। हर त्रिभुज की भुजा-लंबाई पिछले चरण में त्रिभुजों की
परिणामी आकृति को {२४६} {२४४} कोच स्नोफ्लेक {२४५} {२४ after}, स्वीडिश गणितज्ञ {२४}} हेलज वॉन कोच {२४ ९} के नाम पर रखा गया है। ध्यान दें, एक बार फिर, कि {२५०} छोटे खंड {२५१}, हिमखंड के किनारे {२५२} बड़े खंड {२५३} के समान दिखते हैं।
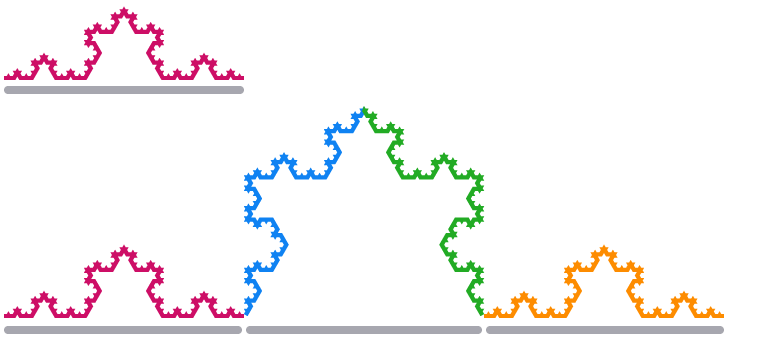
जब हम कोच स्नोफ्लेक के एक किनारे खंड को 3 के कारक से मापते हैं, तो इसकी लंबाई
आयामों और पैमाने कारकों के बीच समान संबंध का उपयोग करते हुए, हमें समीकरण
क्षेत्र
कोच स्नोफ्लेक्स बनाना लगभग एक




पहली पुनरावृत्ति के बाद, हर चरण में
बता दें कि
अनंत
परिधि
हम कोच बर्फ के टुकड़े की परिधि की गणना करने का भी प्रयास कर सकते हैं। जैसा कि हमने पहले ही देखा है, परिधि की लंबाई हर कदम पर
इसका मतलब है कि, एक बार फिर, हमारे पास एक ज्यामितीय श्रृंखला है - लेकिन इस मामले में, यह {३१ ९} नहीं है {३२०}। {३१ {} {}२५} इसका मतलब है कि कोच हिमखंड की परिधि वास्तव में {३१५} अनंत रूप से लंबी {३१६} है! {३१}}

यदि यह प्रतिवाद प्रतीत होता है, तो बस याद रखें कि हम हर चरण में
यह लगभग अकल्पनीय है कि आपके पास परिमित क्षेत्र के साथ एक आकार हो सकता है और एक अनंत परिधि - लेकिन यह भग्न के कई अप्रत्याशित गुणों में से एक है।
क्या आप अपने स्वयं के भग्न बनाने के लिए किसी अन्य तरीके के साथ आ सकते हैं?
"मेरी आत्मा चारों ओर जमे हुए भग्न पर घूम रही है ..."
मेन्जर स्पंज
ऊपर दिए गए कई उदाहरणों की तरह, भग्न को "सपाट" नहीं होना चाहिए। 3-आयामी दिखने वाले सबसे प्रसिद्ध भग्नों में से एक मैसेंजर स्पंज है, जिसका नाम गणितज्ञ
हम एक ठोस घन के साथ शुरू करते हैं, और बार-बार छोटे और छोटे छेद को अपने पक्षों में ड्रिल करते हैं। छिद्रों के प्रत्येक नए पुनरावृत्ति में
A
अब हम मेन्जर स्पंज के आयाम d की गणना करने का प्रयास कर सकते हैं, जैसे हमने ऊपर कोख के बर्फ के टुकड़े के लिए किया था। इस स्थिति में हमें
यदि आप अधिक से अधिक छेदों को काटने की कल्पना करते हैं, तो असीम रूप से कई बार, कोई वास्तविक मात्रा नहीं बचती है। इसीलिए क्यूब "3-आयामी" नहीं है!
फ्रैक्टल कोस्टलाइन्स
हमने अब तक जो भी फ्रैक्टल्स देखे हैं उनमें से एक प्रमुख विशेषता यह है कि आप हमेशा के लिए "ज़ूम इन" कर सकते हैं और हमेशा नए पैटर्न पा सकते हैं। 1920 के आसपास, ब्रिटिश गणितज्ञ
आप देश के मूल आकार के साथ शुरू करते हैं, और, जैसे ही आप ज़ूम इन करते हैं, आप नदी के इनलेट्स, बे और इस्ट्यूरीज़ जोड़ते हैं, फिर व्यक्तिगत चट्टानें, चट्टानें, कंकड़-पत्थर इत्यादि:
किसी देश की सीमा की लंबाई की गणना करने की कोशिश करते समय यह एक महत्वपूर्ण समस्या है - आप कैसे तय करते हैं कि कितनी दूर तक ज़ूम करना है, और किन नुक्कड़ और सारस को शामिल करना है?
एक तरीका है कि हम ब्रिटेन की समुद्र तट की लंबाई को माप सकते हैं, उदाहरण के लिए, एक लंबा शासक लेना है, इसके समुद्र तटों के चारों ओर चलना है, और फिर सभी दूरियों को जोड़ना है।
यदि शासक
हम छोटे और छोटे शासकों के साथ बस जा सकते हैं, और हर बार समुद्र तट की लंबाई के लिए हमारा परिणाम थोड़ा लंबा होगा। पहले की तरह कोच्च स्नोफ्लेक, ऐसा लगता है कि ब्रिटेन का समुद्र तट असीम रूप से लंबा है! इसे अक्सर तट रेखा विरोधाभास कहा जाता है।
कुछ दशकों बाद, गणितज्ञ
ब्रिटेन की तटरेखा निश्चित रूप से "भग्न" दिखती है, लेकिन यह स्व-समान नहीं है, अन्य भग्नों की तरह, जिन्हें हमने पहले देखा था। इसके आकार को खोजने के लिए, हम इसे एक ग्रिड पर खींच सकते हैं और उन कोशिकाओं की संख्या की गणना कर सकते हैं जिनके साथ यह अंतर करता है।
प्रारंभ में, 88 कोशिकाओं को काटना है। यदि हम 2 के कारक द्वारा तटरेखा को मापते हैं, तो 197 प्रतिच्छेद करने वाली कोशिकाएँ हैं - दो बार से अधिक!
के कारक से समुद्र तट का आकार बढ़ गया है। पहले की तरह, इसका मतलब है कि तटरेखा का आयाम है
यदि हम इसे बड़े ग्रिड के साथ दोहराते हैं, तो हम पाते हैं कि ब्रिटेन के समुद्र तट का आयाम वास्तव में लगभग 1.21 है। मैंडलब्रॉट ने महसूस किया कि यह फ्रैक्टल आयाम भी एक आकार की खुरदरापन का एक उपाय है - एक नई अवधारणा, जिसके लिए उन्हें गणित और विज्ञान के कई अन्य क्षेत्रों में महत्वपूर्ण अनुप्रयोग मिले।
नेचर एंड टेक्नोलॉजी में अधिक भिन्न
जबकि सच्चा भग्न कभी प्रकृति में प्रकट नहीं हो सकता है, कई वस्तुएं हैं जो भग्न की तरह लगभग दिखती हैं। हमने पहले से ही पौधे, बर्फ के टुकड़े और समुद्र तट देखे हैं, और यहाँ कुछ और उदाहरण हैं:
मध्य एशिया में पर्वत श्रृंखला
भारत में गंगा नदी का डेल्टा
बिजली के बोल्ट
रेटिना में रक्त वाहिकाएं
यूएसए में ग्रांड कैन्यन
बादल
ये सभी ऑब्जेक्ट पूरी तरह से यादृच्छिक दिखाई दे सकते हैं, लेकिन, भग्न की तरह, एक अंतर्निहित पैटर्न है जो निर्धारित करता है कि वे कैसे बनते हैं। गणित हमें आकृतियों को बेहतर ढंग से समझने में मदद कर सकता है, और फ्रैक्टल्स में चिकित्सा, जीव विज्ञान, भूविज्ञान और मौसम विज्ञान जैसे क्षेत्रों में अनुप्रयोग हैं।
कंप्यूटर जनित भग्न इलाका
उदाहरण के लिए, वीडियो गेम या कंप्यूटर-जनरेटेड फिल्मों में उपयोग किए जाने वाले परिदृश्य और बनावट के रूप में, हम वास्तविक "प्रतियां" बनाने के लिए भग्न का उपयोग कर सकते हैं। इस छवि में पानी, पहाड़ और बादल पूरी तरह से एक कंप्यूटर द्वारा बनाए गए हैं, जिसमें भग्न की मदद से!
और हम डिजिटल छवियों को संपीड़ित करने के लिए, उनके फ़ाइल आकार को कम करने के लिए इस प्रक्रिया को उल्टा भी कर सकते हैं। पहला एल्गोरिदम माइकल बार्न्सले और एलन स्लोन द्वारा 1980 के दशक में विकसित किया गया था, और नए लोगों पर अभी भी शोध किया जा रहा है।