फ्रैक्टल्समंडेलब्रोट सेट

पिछले अध्यायों में हमने जो भी भग्न देखे, वे पुनरावृत्ति की एक प्रक्रिया का उपयोग करके बनाए गए थे: आप एक विशिष्ट पैटर्न के साथ शुरू करते हैं, और फिर आप इसे बार-बार दोहराते हैं।

यह गणित में एक और अवधारणा के समान है जिसे आपने पहले देखा था: पुनरावर्ती अनुक्रम के साथ, आप एक विशिष्ट संख्या के साथ शुरू करते हैं, और फिर आप एक ही पुनरावर्ती सूत्र को लागू करते हैं, फिर से और फिर अगला नंबर पाने के लिए। अनुक्रम।

उदाहरण के रूप में पुनरावर्ती सूत्र xn=xn−12 को लें, और संख्या रेखा पर इसकी शर्तों को प्लॉट करें। आप x0 का मान बदल सकते हैं:

ध्यान दें कि परिणामी अनुक्रम कैसे अलग तरह से व्यवहार कर सकता है, जो शुरुआती मूल्य x0 पर निर्भर करता है:

अब तक, हमने कुछ नया नहीं सीखा है। हालाँकि, लगभग एक शताब्दी पहले, गणितज्ञों ने यह पता लगाना शुरू कर दिया था कि यदि आप वास्तविक संख्या रेखा के बजाय जटिल संख्या का उपयोग करते हैं तो इन अनुक्रमों का क्या होगा। उनकी खोज गणित के सभी में सबसे आश्चर्यजनक और सुंदर परिणाम थे।

जूलिया सेट्स

आज्ञा दें, पहले वाले क्रम का उपयोग करें, xn=xn−12, लेकिन जटिल विमान पर। आप निम्न शर्तों का क्या होता है, यह देखने के लिए आप x0 की स्थिति को आगे बढ़ा सकते हैं। यदि अनुक्रम ऐसा लगता है कि यह रूपांतरित हो जाएगा, तो विमान पर स्थित बिंदु को _{span.pill.blue} नीले {{::: column(width=360) में सम्‍मिलित करें:

कि आप देख सकते हैं, यह क्रम इकाई के सर्कल {जैसा| outside the unit square|above the >>>>x<<<<-axis]] (त्रिज्या के साथ वृत्त, मूल में केंद्रित) के अंदर x0 झूठ [[है।

अब चीजों को थोड़ा और कठिन बनाते हैं। पिछली संख्या को चुकाने के बजाय, हम हर बार एक निरंतर c जोड़ते हैं (जो कि कोई भी जटिल संख्या हो सकती है)। दूसरे शब्दों में, xn=xn−12+c। क्या आपको लगता है कि हम अभी भी अभिसरण का एक चक्र प्राप्त करेंगे? आपको क्या लगता है कि अन्य आकार हम देख सकते हैं? जारी रखें

इस आरेख में, आप x0 की स्थिति और साथ ही c के मूल्य को स्थानांतरित कर सकते हैं:

संख्याओं में रंग करके बनाई गई विभिन्न आकृतियों को जूलिया सेट्स कहा जाता है। उन्हें स्वतंत्र रूप से दो फ्रांसीसी गणितज्ञों, गैस्टन जूलिया और पियरे फतौ द्वारा, 1918 के आसपास स्वतंत्र रूप से खोजा गया था।

उस समय, जूलिया सेट वास्तव में कैसा दिखता था, यह कल्पना करने में मदद करने के लिए कोई कंप्यूटर नहीं थे। जूलिया और फ़तौ जैसे गणितज्ञ उनके बारे में गणितीय रूप से तर्क करने में सक्षम थे, लेकिन वे केवल कभी-कभी किसी न किसी, हाथ से खींचे गए रेखाचित्रों को देखते थे कि वे कैसा दिखते हैं।

आज हमारे पास यह समस्या नहीं है - नीचे दी गई छवियां विभिन्न जूलिया सेटों की हैं। विभिन्न रंग को इंगित करते हैं कि कितनी जल्दी उस बिंदु पर अनुक्रम होता है:

जारी रखें

मंडेलब्रोट सेट

अलग-अलग जूलिया सेट बनाते समय, आपने देखा होगा कि c के कुछ मूल्य थे, जिनके लिए प्रत्येक अनुक्रम डायवर्ज होता है, और संपूर्ण जटिल विमान सफेद रहता है। जूलिया और फतौ के कुछ दशकों बाद, गणितज्ञों की एक नई पीढ़ी ने उन क्षेत्रों को देखने की कोशिश की, जो इन क्षेत्रों में दिखते थे।

पिछले उदाहरण में, हमने c के लिए एक निश्चित मान चुना, और फिर विमान को रंगने के लिए x0 की स्थिति बदल दी। अब x0=0 का मान ठीक करें, और इसके बजाय c का मान बदलें।

एक बार फिर, उस क्षेत्र को प्रकट करने के लिए जटिल विमान पर पेंट करें जिसमें अनुक्रम बंधे हुए हैं। आप किस आकार के दिखने की उम्मीद करते हैं?

xn=xn−12+${complex(c)}

x0=${complex(x0)}

x1=${complex(x1)}

x2=${complex(x2)}

x3=${complex(x3)}

…Bounded!Diverges!

इस भग्न को मैंडलब्रॉट सेट कहा जाता है, और जब 90 ° घुमाया जाता है, तो यह लगभग एक व्यक्ति की तरह दिखता है, जिसमें सिर, शरीर और दो भुजाएँ होती हैं। इसे 1978 में गणितज्ञ रॉबर्ट ब्रूक्स और पीटर मैटेस्की द्वारा एक शोध पत्र में पहली बार परिभाषित और तैयार किया गया था:

कुछ साल बाद, बेनोइट मैंडलब्रॉट ने आईबीएम के शक्तिशाली कंप्यूटरों का उपयोग फ्रैक्टल के बहुत अधिक विस्तृत दृश्य बनाने के लिए किया, जिसे बाद में उनके नाम पर रखा गया। पहला प्रिंटआउट उसकी अपेक्षा से भिन्न था - जब तक कि उसने महसूस किया कि प्रिंटर पर काम करने वाले तकनीशियन उसके किनारे के चारों ओर "फ़िज़नेस" की सफाई कर रहे थे, यह मानते हुए कि यह धूल के कणों या प्रिंटर त्रुटियों के कारण हुआ था, न कि भग्न की एक विशिष्ट विशेषता। ! जारी रखें

सभी फ्रैक्टल्स की तरह, हम "जूम इन" मेंडलब्रॉट को हमेशा के लिए सेट कर सकते हैं, हर पैमाने पर नए पैटर्न ढूंढ रहे हैं। यहां आप मंडेलब्रोट सेट के एक हिस्से को ज़ूम कर सकते हैं जिसे सीहोरस घाटी कहा जाता है। ब्लैक पॉइंट_ के अंदर_ मैंडलब्रॉट सेट हैं, जहां अनुक्रम बाउंड है। रंगीन अंक के बाहर मैंडलब्रॉट सेट हैं, जहां अनुक्रम डायवर्ज होता है, और अलग-अलग रंग इंगित करते हैं कि कितनी जल्दी यह अनंत तक बढ़ता है:

Scale: ${pow(scale)}

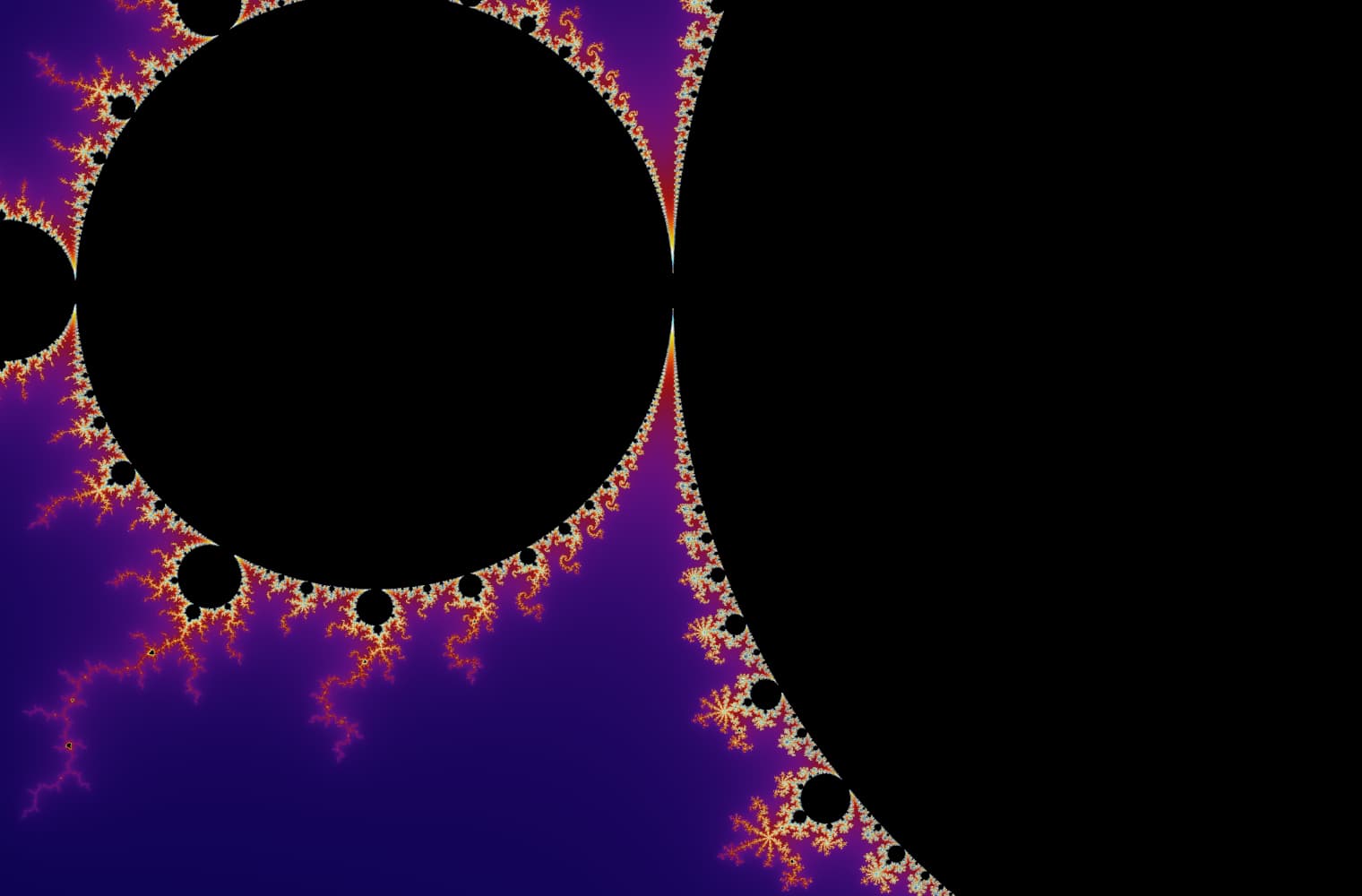
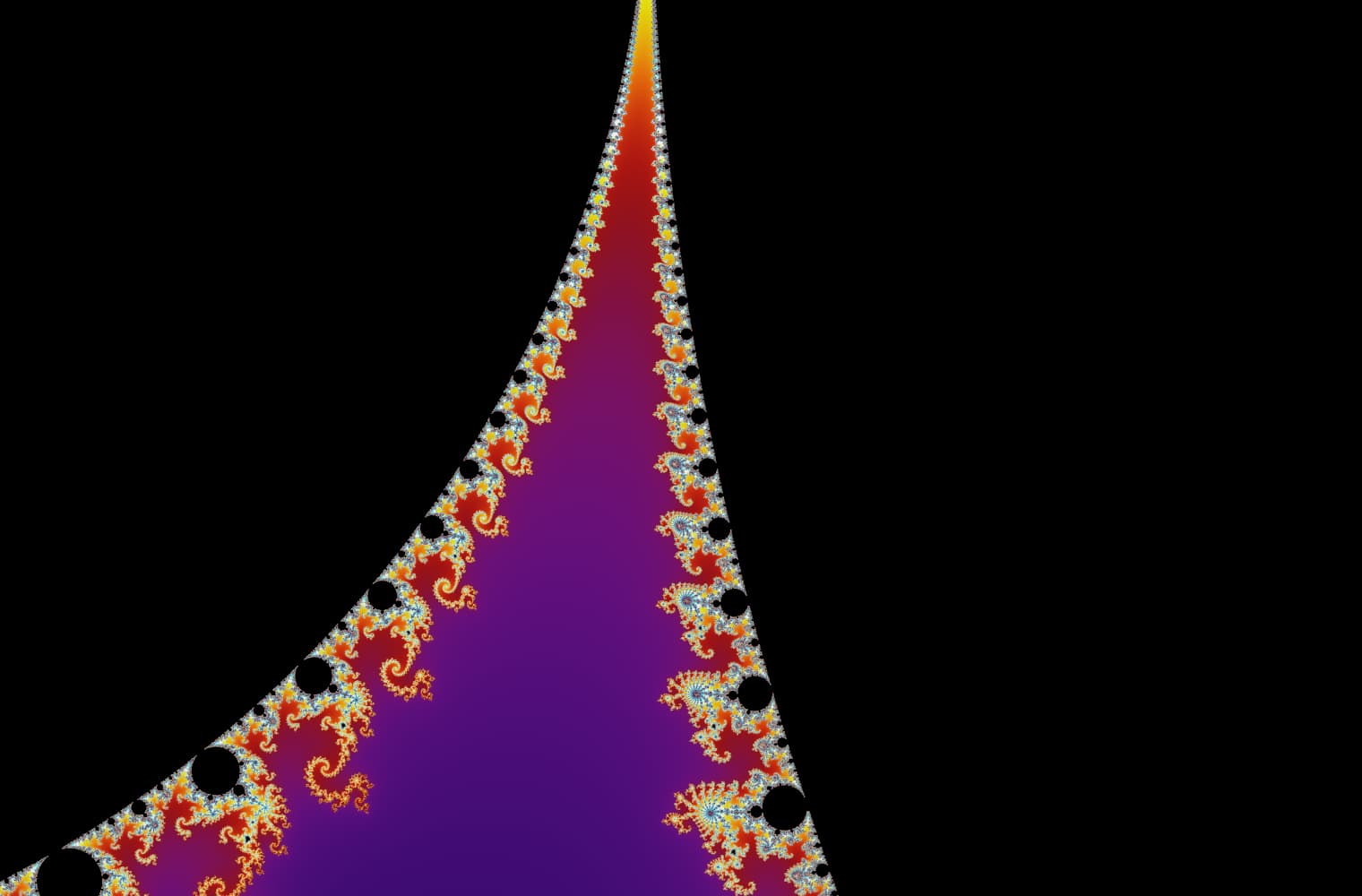
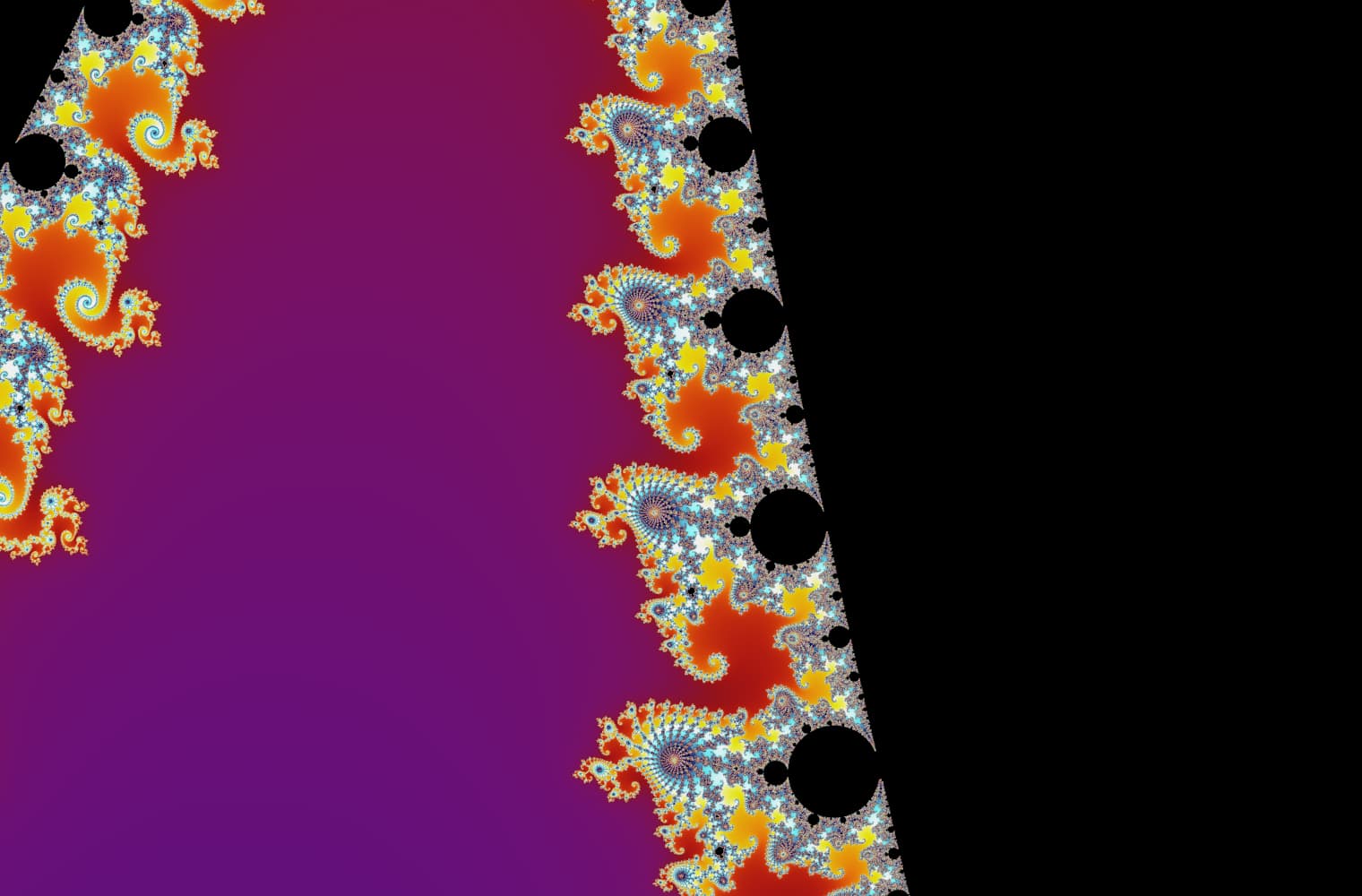
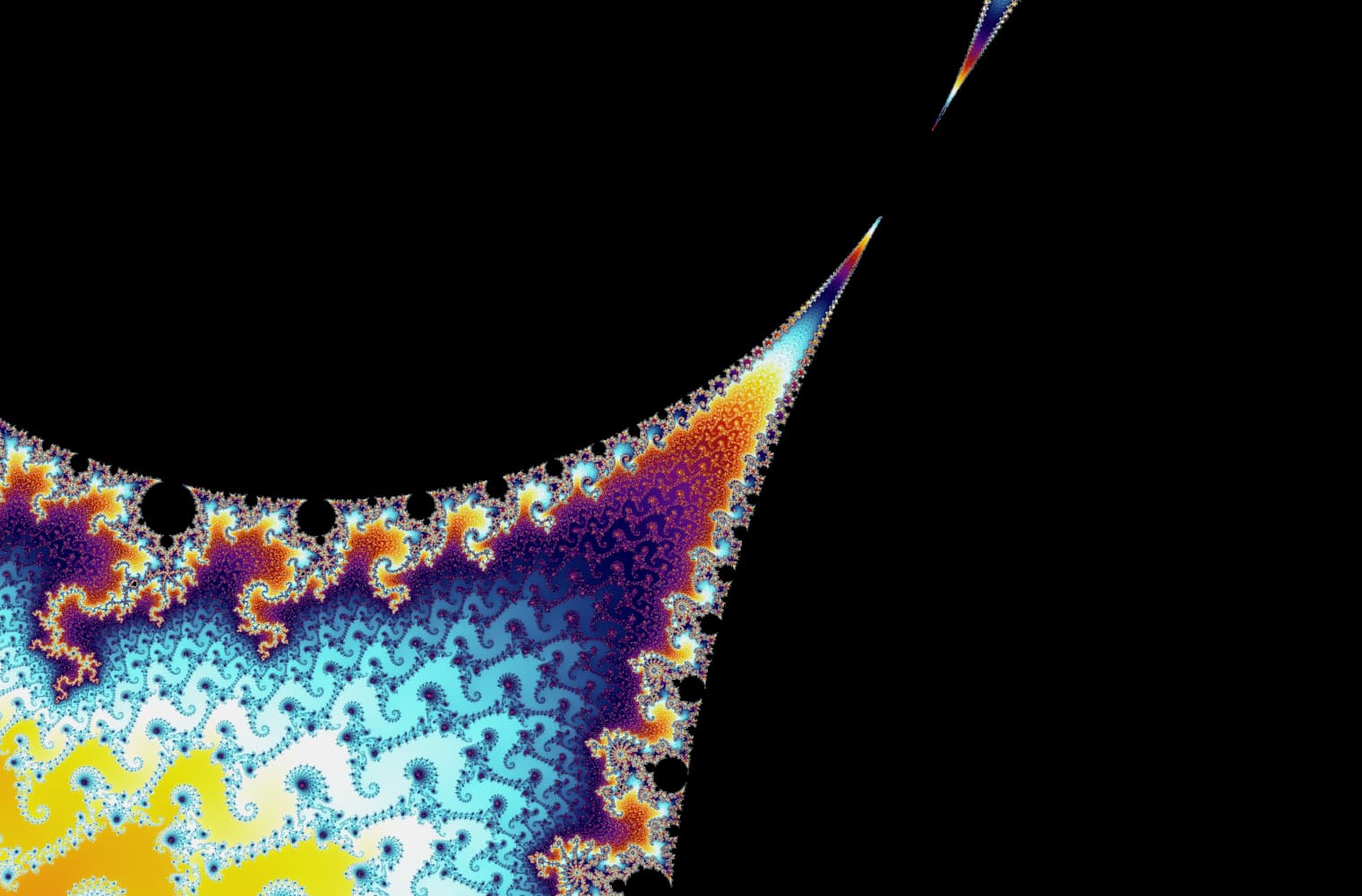
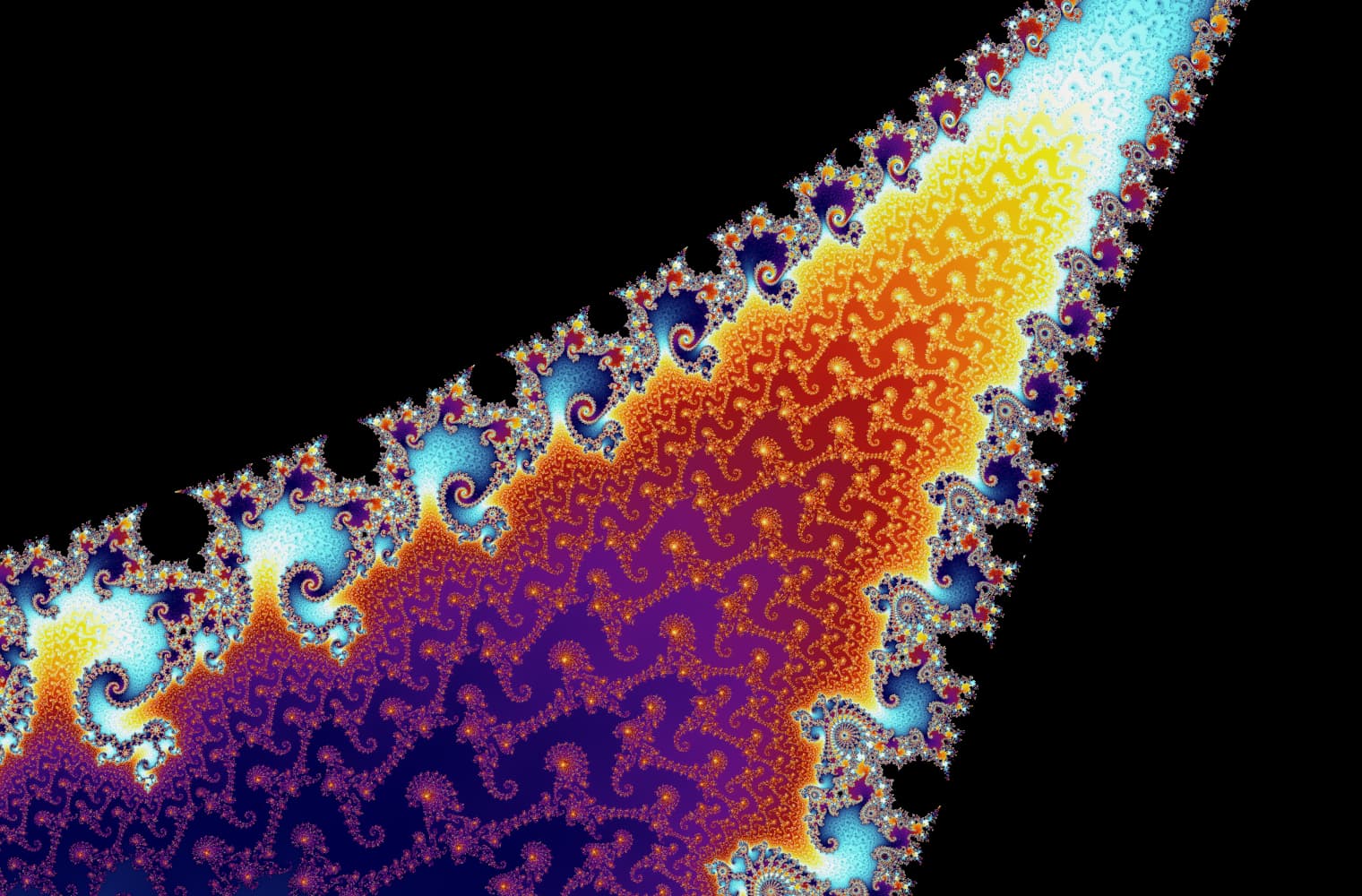
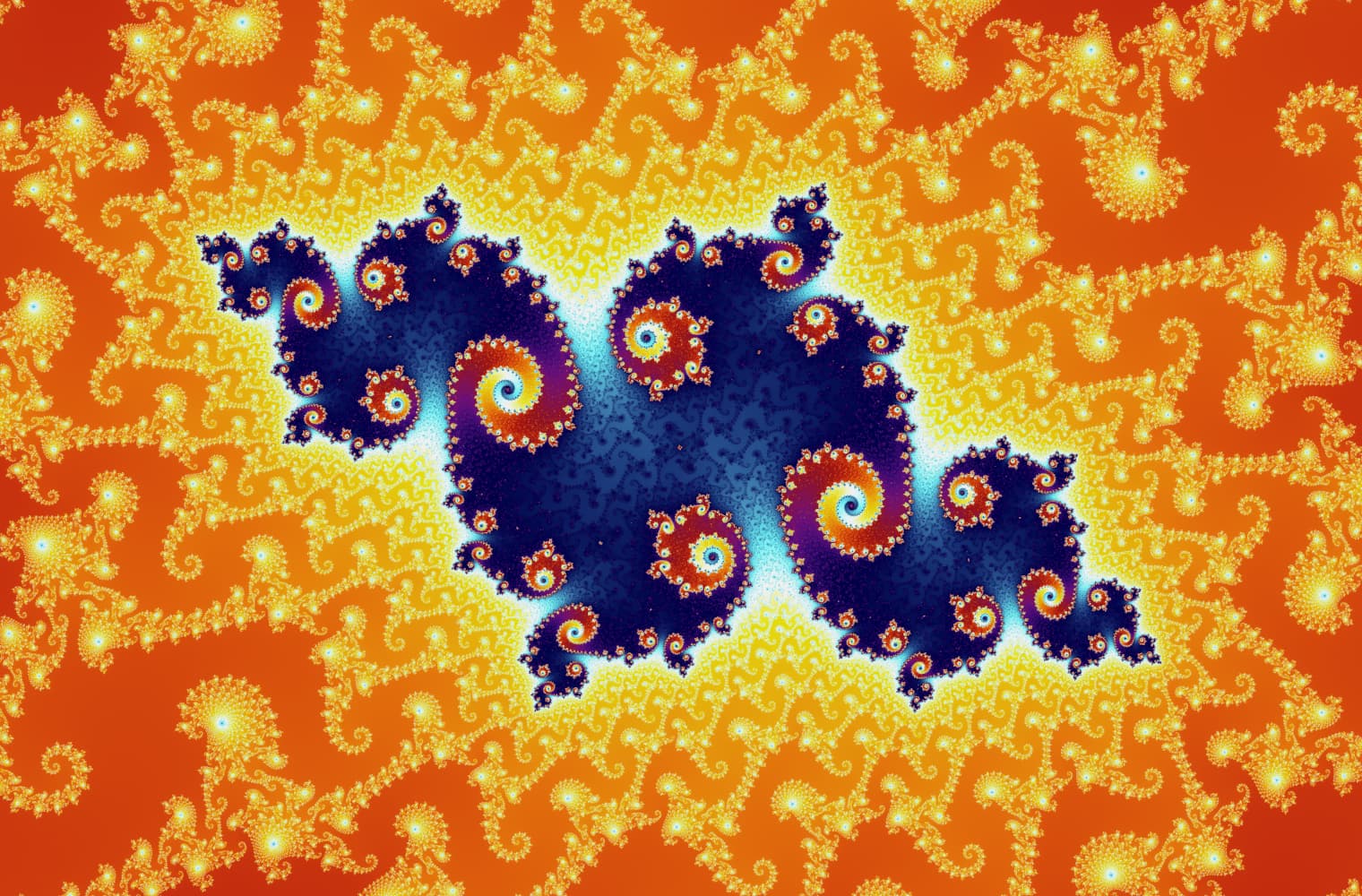
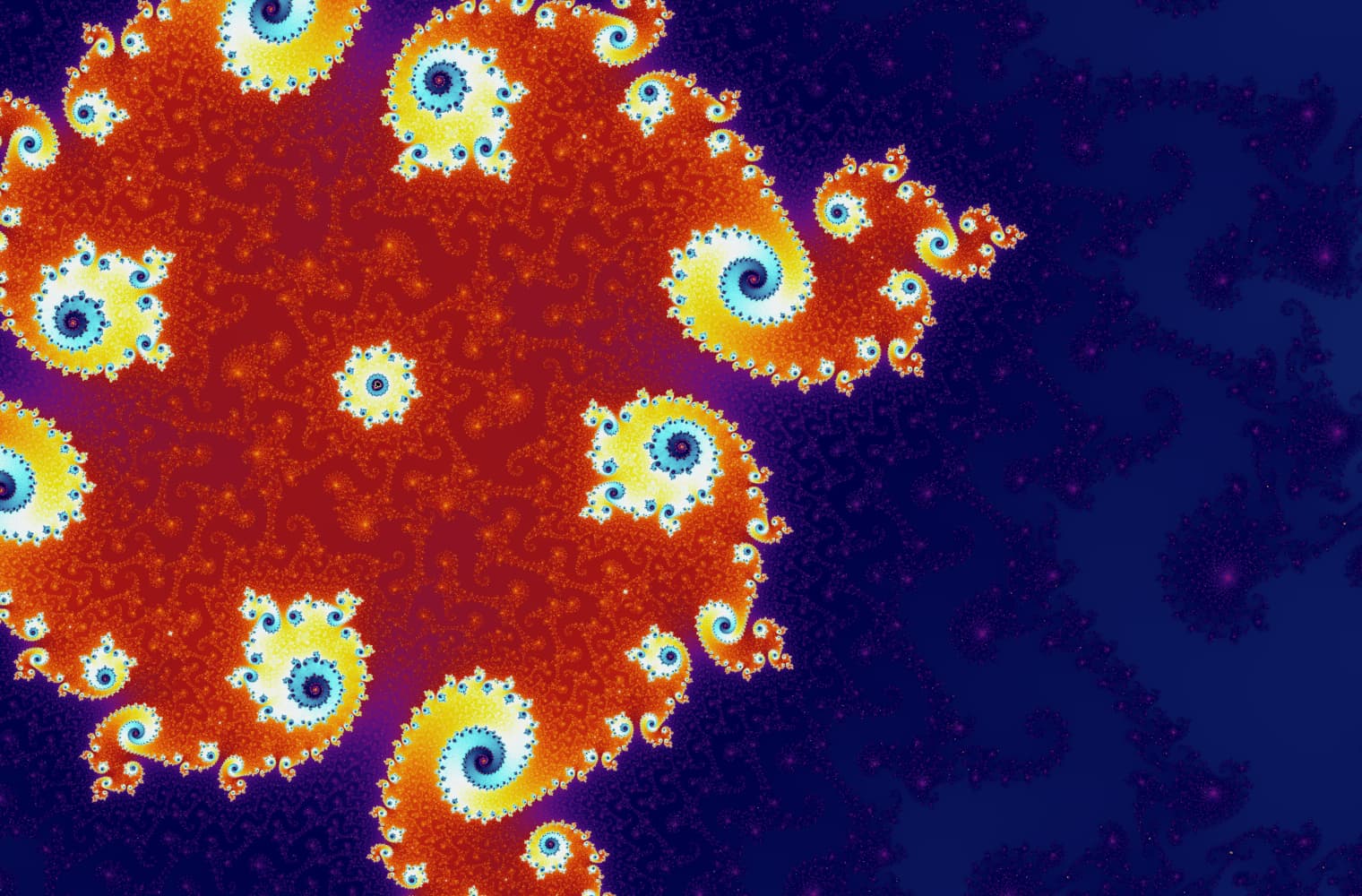
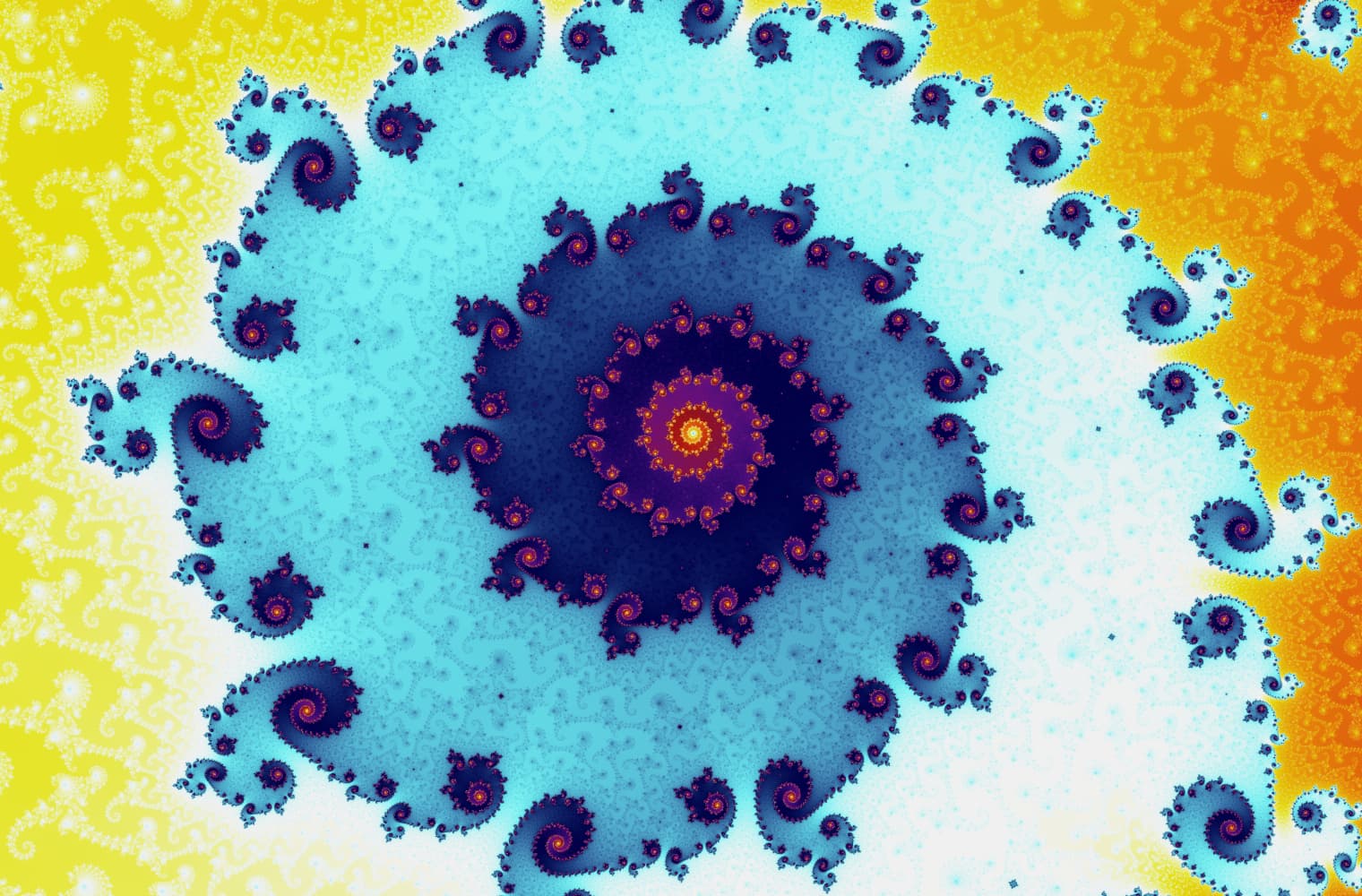
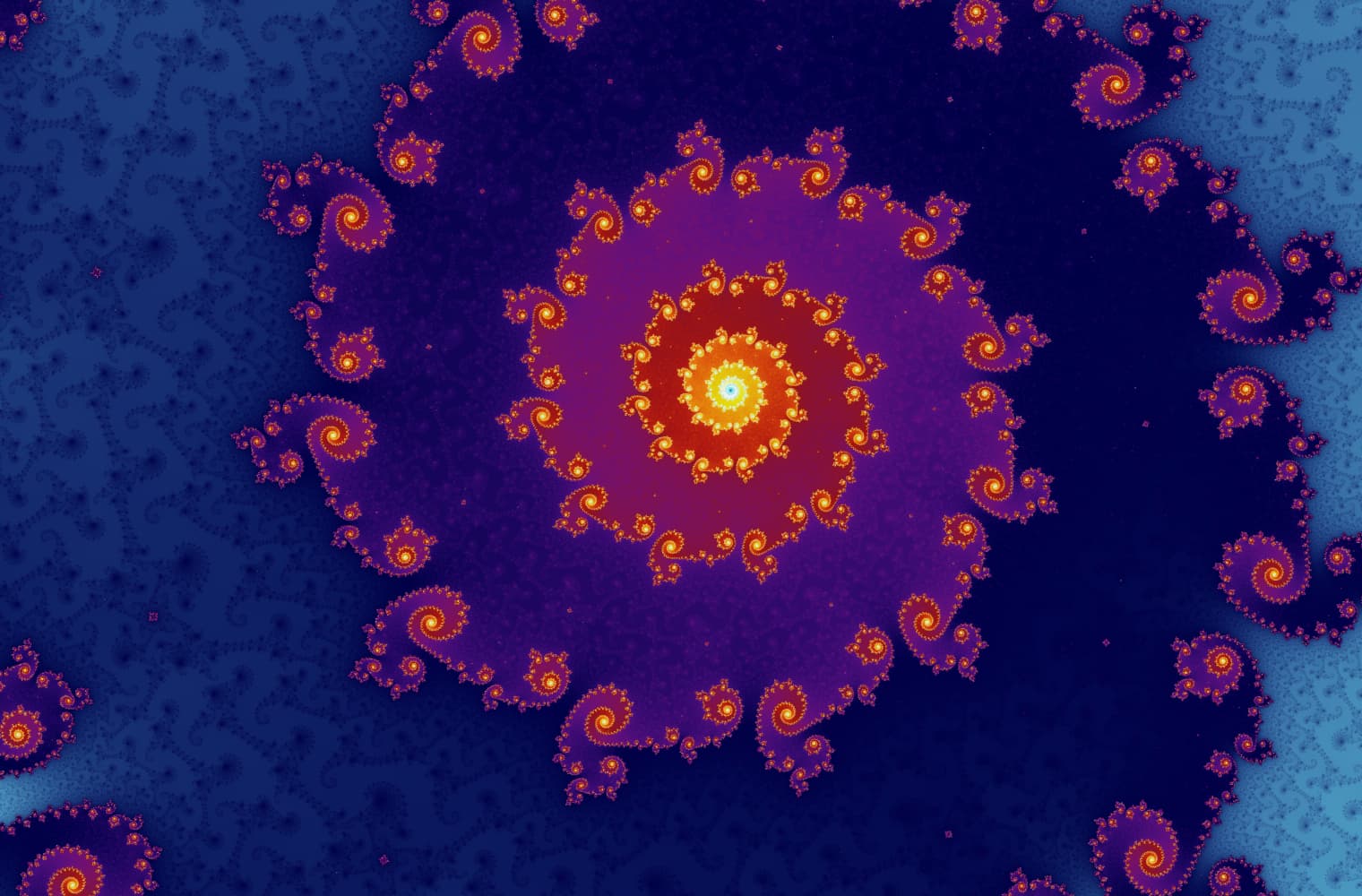
इस स्लाइडर में 27 व्यक्तिगत छवियां शामिल हैं, 14 क्वाड्रिलियन से अधिक ज़ूम स्तर तक, या 254। कुल मिलाकर, आधुनिक लैपटॉप पर रेंडर करने में उन्हें लगभग 45 मिनट लगे। मैंडलब्रॉट सेट को एक एकल, सरल समीकरण xn=xn−12+c के साथ बनाया जा सकता है, फिर भी यह असीम रूप से जटिल और आश्चर्यजनक सुंदर है।

जैसे ही आप Mandelbrot सेट के चारों ओर c का मान बढ़ाते हैं, आपको एक जिज्ञासु संपत्ति दिखाई दे सकती है:

• मैंडेलब्रॉट सेट के मुख्य शरीर के भीतर सभी अनुक्रमdivergereach an orbit को एक बिंदु पर परिवर्तित करते हैं।
• बड़े बल्ब शीर्ष अंक_ से मिलकर|converge|diverge]] _{span.reveal(when="blank-1")} एक कक्षा में पहुंचते हैं।
• क्रम में इस छोटे बल्ब की लंबाई की परिक्रमा है।

२४प्रत्येक बल्ब की एक अलग आकार की कक्षा होती है, जिसमें छोटे बल्ब अपनी कक्षाओं में अधिक से अधिक अंक रखते हैं। इन कक्षाओं का आकार लॉजिस्टिक मैप से संबंधित है, कैओस सिद्धांत में एक महत्वपूर्ण अवधारणा है।