रूपांतरण और समरूपतासमरूपता समूह और वॉलपेपर
कुछ आकृतियों में एक से अधिक समरूपता होती है - चलो एक सरल उदाहरण के रूप में








आपने पहले ही ऊपर दिखाया है कि एक वर्ग में प्रतिबिंब के
इसमें
और अंत में, हम एक और विशेष प्रकार की समरूपता के रूप में "कुछ नहीं करने" के बारे में सोच सकते हैं - क्योंकि परिणाम (स्पष्ट रूप से) पहले जैसा ही है। इसे कभी-कभी पहचान भी कहा जाता है।
कुल मिलाकर, हमने
अब हम वास्तव में इन समरूपताओं के साथ कुछ अंकगणित करना शुरू कर सकते हैं। उदाहरण के लिए, हम नया पाने के लिए दो समरूपता जोड़ सकते हैं:






जब भी आप एक वर्ग के दो समरूपता जोड़ते हैं, तो आपको एक नया मिलता है। यहाँ एक "समरूपता कैलकुलेटर" है जहाँ आप इसे स्वयं आज़मा सकते हैं:
समरूपता कैलकुलेटर के साथ खेलने के लिए कुछ समय बिताएं, और किसी भी पैटर्न को खोजने की कोशिश करें। क्या आप इन टिप्पणियों को पूरा कर सकते हैं?
- दो घुमाव जोड़ने से हमेशा
(या पहचान)। * दो प्रतिबिंबों को जोड़ना हमेशा (या पहचान)। * विपरीत क्रम में एक ही दो समरूपता जोड़ना परिणाम । * पहचान जोड़ने से ।
आप पहले से ही महसूस कर रहे होंगे कि जोड़ना समरूपता वास्तव में जोड़ने के समान है पूर्णांक :
- Adding two symmetries/integers always gives another symmetry/integer:
+ = 12 + 7 = 19 - Adding symmetries/integers is
associative :+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Every symmetry/integer has an inverse, another symmetry/integer which, when added, gives the identity:
+ = 4 + –4 = 0
गणित में, किसी भी संग्रह में, जिसमें ये गुण हैं, एक
इस उदाहरण में, हमने वर्ग के आठ समरूपों के साथ शुरुआत की। वास्तव में, हर ज्यामितीय आकार का अपना समरूप समूह होता है । उन सभी में अलग-अलग तत्व हैं, लेकिन वे हमेशा उपरोक्त तीन नियमों को पूरा करते हैं।
गणित में हर जगह समूह दिखाई देते हैं। तत्व संख्या या समरूपता हो सकते हैं, लेकिन साथ ही बहुपद, क्रमपरिवर्तन, मेट्रिसेस, फ़ंक्शंस ... कुछ भी जो तीन नियमों का पालन करते हैं। समूह सिद्धांत का मुख्य विचार यह है कि हम व्यक्तिगत तत्वों में रुचि नहीं रखते हैं, बस इस तरह से वे एक दूसरे के साथ बातचीत करते हैं ।
उदाहरण के लिए, विभिन्न अणुओं के समरूपता समूह वैज्ञानिकों को संबंधित सामग्रियों के गुणों की भविष्यवाणी और व्याख्या करने में मदद कर सकते हैं।
समूह का उपयोग बोर्ड गेम में जीतने की रणनीति, चिकित्सा में वायरस के व्यवहार, संगीत में विभिन्न सामंजस्य और अन्य अन्य कार्यों के विश्लेषण के लिए भी किया जा सकता है ...
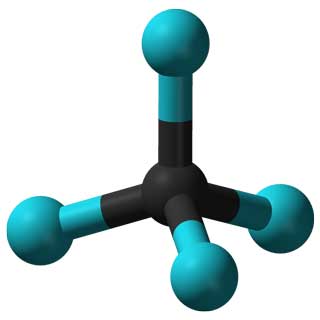
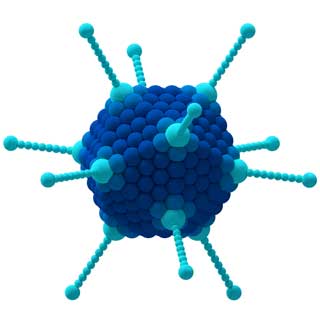
CCl 4 अणु (बाएं) और एडेनोवायरस (दाएं) के गुण उनके समरूपता से निर्धारित होते हैं।
वॉलपेपर समूह
पिछले खंडों में हमने दो अलग-अलग परिवर्तनों के अनुरूप दो अलग-अलग प्रकार की समरूपता देखी: घुमाव और प्रतिबिंब। लेकिन तीसरे प्रकार के कठोर परिवर्तन के लिए एक समरूपता भी है:


हेक्सागोनल होनीकोम्ब


सिरेमिक दीवार टाइलिंग
रिफ्लेक्शनल, रोटेशनल और ट्रांसलेशनल सिमेट्री के अलावा, यहां तक कि चौथा प्रकार है:


एक पैटर्न में एक से अधिक प्रकार की समरूपता हो सकती है। और वर्गों के लिए की तरह, हम एक पैटर्न के
ये समूह आपको इस बारे में ज़्यादा नहीं बताते कि पैटर्न कैसा दिखता है (जैसे इसके रंग और आकार), बस इसे कैसे दोहराया जाता है । कई अलग-अलग पैटर्न में समान समरूपता समूह हो सकता है - जब तक कि एक ही तरीके से व्यवस्थित और दोहराया नहीं जाता है।


इन दोनों पैटर्न में समान समरूपताएं हैं, भले ही वे बहुत अलग दिखें। लेकिन समरूपता रंगों, या सतही आकृतियों के बारे में नहीं है।


इन दो पैटर्न में समान समरूपताएं हैं - भले ही वे एक दूसरे की तुलना में बाईं ओर इसी पैटर्न के समान दिखते हैं।
यह पता चला है कि, जबकि असीम रूप से कई संभावित पैटर्न हैं, उन सभी में सिर्फ 17 अलग-अलग समरूपता समूह हैं। इन्हें वॉलपेपर समूह कहा जाता है। हर वॉलपेपर समूह अनुवाद, घुमाव, प्रतिबिंब और ग्लाइड प्रतिबिंब के संयोजन से परिभाषित होता है। क्या आप इन उदाहरणों में

Group 1 – P1
Only translations div img(src="/content/transformations/images/wallpapers/p2.svg" width=360, height=240) p.caption Group 2 – P2 Rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p3.svg" width=360, height=240) p.caption Group 3 – P3 Rotations of order 3 (120°), translations div img(src="/content/transformations/images/wallpapers/p4.svg" width=360, height=240) p.caption Group 4 – P4 Four rotations of order 2 (180°), translations div img(src="/content/transformations/images/wallpapers/p6.svg" width=360, height=240) p.caption Group 5 – P6 Rotations of order 2, 3 and 6 (60°), translations div img(src="/content/transformations/images/wallpapers/pm.svg" width=360, height=240) p.caption Group 6 – PM Parallel axes of reflection, translations div img(src="/content/transformations/images/wallpapers/pmm.svg" width=360, height=240) p.caption Group 7 – PMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p4m.svg" width=360, height=240) p.caption Group 8 – P4M Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p6m.svg" width=360, height=240) p.caption Group 9 – P6M Rotations (ord 2 + 6), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p3m1.svg" width=360, height=240) p.caption Group 10 – P3M1 Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p31m.svg" width=360, height=240) p.caption Group 11 – P31M Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p4g.svg" width=360, height=240) p.caption Group 12 – P4G Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/cmm.svg" width=360, height=240) p.caption Group 13 – CMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pmg.svg" width=360, height=240) p.caption Group 14 – PMG Reflections, glide reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pg.svg" width=360, height=240) p.caption Group 15 – PG Parallel glide reflections, translations div img(src="/content/transformations/images/wallpapers/cm.svg" width=360, height=240) p.caption Group 16 – CM Reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/pgg.svg" width=360, height=240) p.caption Group 17 – PGG Perpendicular glide reflections, rotations of order 2, translations
दुर्भाग्य से कोई सरल कारण नहीं है कि इनमें से 17 समूह क्यों हैं, और यह साबित करने के लिए अधिक उन्नत गणित की आवश्यकता है। इसके बजाय, आप 17 वॉलपेपर समूहों में से प्रत्येक के लिए अपने खुद के दोहराया पैटर्न खींचने की कोशिश कर सकते हैं:
Examples of other students’ drawings



वॉलपेपर समूह सभी फ्लैट, द्वि-आयामी पैटर्न के बारे में थे। हम त्रि-आयामी पैटर्न के लिए कुछ समान कर सकते हैं: इन्हें क्रिस्टलोग्राफिक समूह कहा जाता है, और इनमें से 219 हैं!
अनुवाद, प्रतिबिंब, घुमाव और ग्लाइड प्रतिबिंब के अलावा, इन समूहों में ग्लाइड विमानों और स्क्रू कुल्हाड़ियों जैसे समरूपता शामिल हैं (बोतल को हटाते समय गति के बारे में सोचें)।
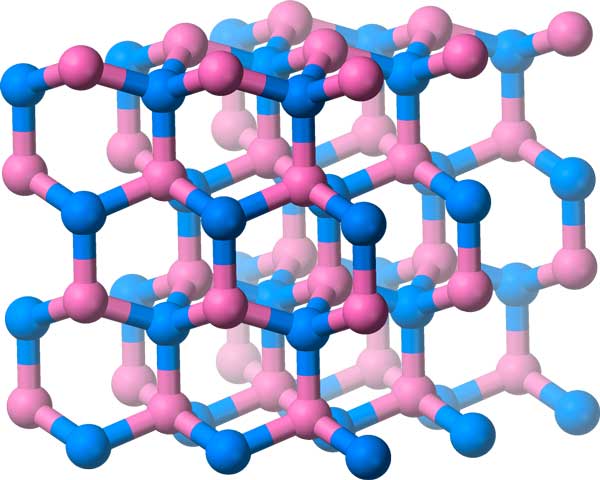
बोरॉन-नाइट्राइड में इस क्रिस्टल जाली में अपने अणुओं की व्यवस्था है, जिसमें तीन आयामी समरूपता समूह है।