बहुभुज और पॉलीहेड्राtessellations

बहुभुज प्रकृति में हर जगह दिखाई देते हैं। यदि आप एक बड़े क्षेत्र को टाइल करना चाहते हैं तो वे विशेष रूप से उपयोगी हैं, क्योंकि आप बिना किसी अंतराल या ओवरलैप के पॉलीगॉन को एक साथ फिट कर सकते हैं। उस तरह के पैटर्न को tessellations कहा जाता है।

प्राचीन रोम से लेकर वर्तमान तक - मनुष्य ने कला, वास्तुकला और प्रौद्योगिकी में इनमें से कई प्राकृतिक पैटर्न की नकल की है। कुछ उदाहरण निम्नलिखित हैं:

यहां आप नियमित बहुभुज का उपयोग करके अपने खुद के टेसल्स बना सकते हैं। बस कैनवास पर साइडबार से नए आकार खींचें। कौन सा आकार टेसलेट को अच्छी तरह से आकार देता है? वहाँ किसी भी आकार कि सब पर tessellate नहीं कर रहे हैं? दिलचस्प पैटर्न बनाने की कोशिश करें!

Examples of other students’ tessellations

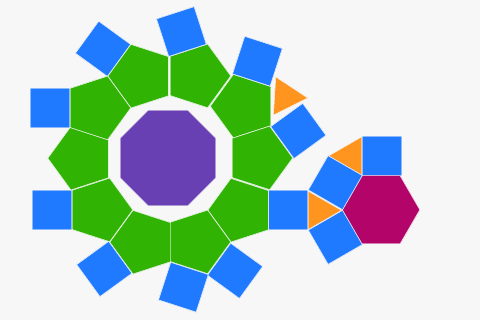
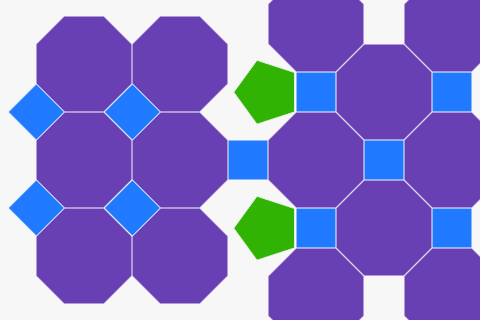
नियमित बहुभुजों से टेसल्स

आपने देखा होगा कि कुछ नियमित बहुभुज (जैसे वर्ग) पेंटागन ) बहुत आसानी से टेसलेट करते हैं, जबकि अन्य ( तरह) त्रिभुज हेक्सागोन्स ) बिल्कुल भी नहीं लगता।

यह उनके आंतरिक कोण के आकार के साथ करना है, जिसे हमने पहले गणना करना सीखा था। टेस्यूलेशन में प्रत्येक शीर्ष पर, कई अलग-अलग बहुभुजों के आंतरिक कोण मिलते हैं। हमें डिग्री तक जोड़ने के लिए इन सभी कोणों की आवश्यकता है, अन्यथा या तो एक अंतराल या एक ओवरलैप होगा।

आप इसी तरह जाँच सकते हैं कि, पेंटागन की तरह, 7 या अधिक पक्षों के साथ कोई भी नियमित बहुभुज tessellate नहीं करता है। इसका मतलब यह है कि केवल नियमित बहुभुज जो कि टेसेलेट त्रिकोण, वर्ग और हेक्सागोन हैं!

निश्चित रूप से आप विभिन्न प्रकार के नियमित बहुभुजों को एक कटाव में जोड़ सकते हैं, बशर्ते कि उनके आंतरिक कोण 360 को जोड़ सकते हैं:

Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°

Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°

Hexagons and triangles
120° + 120° + 60° + 60° = 360°

Hexagons and triangles
120° + 60° + 60° + 60° + 60° = 360°

Hexagons, squares and triangles
120° + 90° + 90° + 60° = 360°

Octagons and squares
135° + 135° + 90° = 360°

Dodecagons (12-gons) and triangles
150° + 150° + 60° = 360°

Dodecagons, hexagons and squares
150° + 120° + 90° = 360°

अनियमित बहुभुजों से तनाव

हम अनियमित बहुभुजों के बाहर टेस्यूलेशन बनाने की भी कोशिश कर सकते हैं - जब तक हम उन्हें घुमाते और व्यवस्थित करते समय सावधान रहते हैं।

पेंटागन थोड़ा पेचीदा है। हमने पहले ही देखा कि नियमित पेंटागन टेसलेट नहीं करते हैं tessellate , लेकिन गैर-नियमित लोगों के बारे में क्या?

यहाँ पेंटागन के साथ tessellations के तीन अलग-अलग उदाहरण हैं। वे नियमित नहीं हैं, लेकिन वे पूरी तरह से 5-पक्षीय बहुभुज हैं।

अब तक, गणितज्ञों ने केवल 15 अलग-अलग प्रकार के tessellations पाए हैं (उत्तल) पेंटागन के साथ - जिनमें से सबसे हाल ही में 2015 में खोजा गया था। कोई नहीं जानता कि क्या कोई अन्य है, या यदि ये 15 ही हैं ...

कला में Tessellations

Tessellations हम दोनों कई कलाकारों, वास्तुकारों और डिजाइनर के लिए एक उपकरण और प्रेरणा - सबसे प्रसिद्ध डच कलाकार MC Escher हैं । एस्चर के काम में अजीब, उत्परिवर्ती जीव, पैटर्न और परिदृश्य शामिल हैं:

ये कलाकृतियाँ अक्सर मज़ेदार और सहज लगती हैं, लेकिन अंतर्निहित गणितीय सिद्धांत पहले जैसे ही हैं: कोण, घुमाव, अनुवाद और बहुभुज। अगर गणित सही नहीं है, तो टेस्यूलेशन काम नहीं करेगा!

“Metamorphosis II” by M. C. Escher (1940)

पेनरोज़ टिलिंग्स

अब तक हमने जितने भी टेस्यूलेशन देखे, उनमें एक चीज समान है: वे आवधिक हैं । इसका मतलब है कि उनके पास एक नियमित पैटर्न है जो बार-बार दोहराया जाता है। वे सभी दिशाओं में हमेशा के लिए जारी रख सकते हैं और वे हर जगह समान दिखेंगे।

1970 के दशक में, ब्रिटिश गणितज्ञ और भौतिक विज्ञानी रोजर पेनरोज़ ने गैर-आवधिक तनावों की खोज की - वे अभी भी सभी दिशाओं में असीम रूप से जारी हैं, लेकिन कभी भी एक समान नहीं दिखते हैं। इन्हें पेनरोज़ टिलिंग्स कहा जाता है, और आपको केवल एक बनाने के लिए कुछ अलग प्रकार के बहुभुजों की आवश्यकता होती है:

पेनरोज़ विशुद्ध रूप से मनोरंजन के लिए टेस्यूलेशन की खोज कर रहे थे, लेकिन यह पता चला कि कुछ वास्तविक सामग्रियों (जैसे एल्यूमीनियम) की आंतरिक संरचना एक समान पैटर्न का पालन करती है। टॉयलेट पेपर पर भी पैटर्न का उपयोग किया गया था, क्योंकि निर्माताओं ने देखा कि एक गैर-आवधिक पैटर्न को बिना किसी उभार के रोल किया जा सकता है।