बहुभुज और पॉलीहेड्राप्लैटोनिक सॉलिड्स

इस पाठ्यक्रम की शुरुआत में हमने नियमित बहुभुजों को विशेष रूप से "सममित" बहुभुज के रूप में परिभाषित किया, जहां सभी पक्ष और कोण समान हैं। हम पॉलीहेड्रा के लिए कुछ ऐसा ही कर सकते हैं।

एक नियमित बहुतल में सभी चेहरे सभी नियमित बहुभुज के एक ही तरह है, और हर शिखर पर चेहरे मिलने की एक ही नंबर है। इन दो गुणों वाले पॉलीहेड्रा को प्लेटोनिक ठोस कहा जाता है, जिसका नाम ग्रीक दार्शनिक प्लेटो के नाम पर रखा गया है।

तो प्लेटोनिक ठोस क्या दिखते हैं - और उनमें से कितने हैं? त्रि-आयामी आकार बनाने के लिए, हमें प्रत्येक शीर्ष पर मिलने के लिए कम से कम चेहरे चाहिए। आइए व्यवस्थित रूप से सबसे छोटे नियमित बहुभुज से शुरू करें: समबाहु त्रिकोण:

और प्रत्येक शीर्ष पर सात या अधिक त्रिभुज भी नए पॉलीहेड्रा का उत्पादन नहीं करते हैं: एक वर्टेक्स के चारों ओर पर्याप्त जगह नहीं है, जिससे कि कई त्रिभुज फिट हो सकें।

इसका मतलब है कि हमने त्रिभुजों से मिलकर प्लेटोनिक ठोस देखे हैं। चलो अगले नियमित बहुभुज पर चलते हैं: वर्ग।

अगला, नियमित रूप से पेंटागन आज़माएँ:

अगर हर शिखर पर पेंटागन मिलते हैं, तो हमें डोडेकेहेड्रोन मिलता है। इसके चेहरे हैं। ("Dodeca" का अर्थ ग्रीक में "बारह" है)

अगले नियमित बहुभुज की कोशिश हेक्सागोन्स हैं:

यदि तीन हेक्सागोन्स हर शीर्ष पर मिलते हैं, तो हम तुरंत एक प्राप्त करते हैं बहुतल हेक्साहेड्रॉन । चूंकि तीन से अधिक के लिए कोई स्थान नहीं है, ऐसा लगता है कि हेक्सागोन से मिलकर प्लैटोनिक ठोस नहीं हैं।

छह से अधिक पक्षों वाले सभी नियमित बहुभुजों के लिए भी यही होता है। वे टेसलेट नहीं करते हैं, और हमें निश्चित रूप से कोई तीन आयामी बहुभुज नहीं मिलते हैं।

इसका मतलब है कि सिर्फ प्लैटोनिक ठोस हैं! आइए एक साथ उन सभी पर एक नज़र डालें:

ध्यान दें कि चेहरे और कोने की संख्या को कैसे अदला-बदली किया जाता है क्यूब और ऑक्टाहेड्रोन के लिए , साथ ही डोडेकेहेड्रोन और इकोसैहेड्रॉन , जबकि किनारों की संख्या समान रहती है अलग हैं । प्लेटोनिक ठोस के इन जोड़े को दोहरे ठोस कहा जाता है।

हम एक पॉलीहेड्रॉन को उसके दोहरे में बदल सकते हैं, "हर जगह" को एक शीर्ष के साथ, और प्रत्येक शीर्ष को एक चेहरे के साथ बदल सकते हैं। ये एनिमेशन दिखाते हैं कि:

टेट्राहेड्रॉन अपने आप में दोहरी है। चूँकि इसमें समान संख्या में चेहरे और कोने हैं, इसलिए उन्हें स्वैप करने से कुछ भी नहीं बदलेगा।

प्लेटो का मानना था कि ब्रह्मांड के सभी पदार्थों में चार तत्व शामिल हैं: वायु, पृथ्वी, जल और अग्नि। उसने सोचा था कि प्रत्येक तत्व प्लेटोनिक ठोस में से एक के अनुरूप है, जबकि पांचवां एक पूरे के रूप में ब्रह्मांड का प्रतिनिधित्व करेगा। आज हम जानते हैं कि 100 से अधिक विभिन्न तत्व हैं जिनमें गोलाकार परमाणु होते हैं, न कि पॉलीहेड्रा।

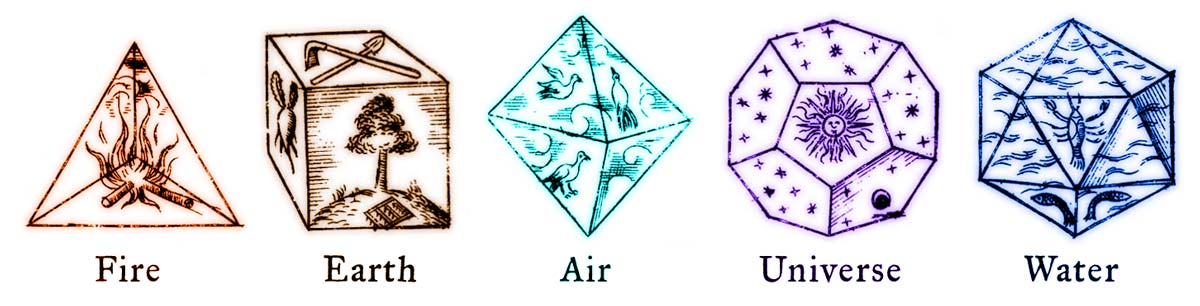
Images from Johannes Kepler’s book “Harmonices Mundi” (1619)

आर्किमिडीज सॉलिड्स

प्लेटोनिक ठोस विशेष रूप से महत्वपूर्ण पॉलीहेड्रा हैं, लेकिन अनगिनत अन्य हैं।

उदाहरण के लिए, आर्किमिडीज़ ठोस , अभी भी नियमित बहुभुजों से बना है , लेकिन आप कई अलग-अलग प्रकारों का उपयोग कर सकते हैं। उनका नाम एक अन्य यूनानी गणितज्ञ के नाम पर रखा गया, आर्किमिडीज ऑफ सिरैक्यूज़ , और उनमें से 13 हैं:

अनुप्रयोग

प्लेटो यह मानने में गलत था कि सभी तत्वों में प्लेटोनिक ठोस होते हैं। लेकिन नियमित पॉलीहेड्रा में कई विशेष गुण होते हैं जो उन्हें प्रकृति में कहीं और दिखाई देते हैं - और हम इन गुणों को विज्ञान और इंजीनियरिंग में कॉपी कर सकते हैं।